8.6. Применение парного линейного уравнения регрессии
Прежде чем обсуждать вопросы использования уравнений парной регрессии, напомним, что парный корреляционный анализ не дает чистых мер влияния только одного изучаемого фактора. Если факторы взаимосвязаны, то парная связь измеряет влияние данного фактора и часть влияния прочих факторов, связанных с ним. И все же при тесной связи уравнение регрессии может стать полезным орудием анализа экономических, технологических, социальных или природных процессов.
Сравнивая фактические уровни надоя в табл. 8.1 с расчетными, т. е. такими, которые были бы получены при фактических затратах средств на корову и средней по совокупности эффективности, измеряемой коэффициентом регрессии, можно найти отклонения уi –?уi. Они показывают, насколько хозяйство получило от коров больше или меньше молока в условиях фактической эффективности использования средств, чем при средней по совокупности эффективности использования средств. Так, в хозяйстве № 6 получено от коровы в среднем 31,8 ц молока, хотя при низком уровне затрат 1355 руб. на корову и средней эффективности затрат было бы получено только по 26,5 ц молока. Фактически надой составил 120% к расчетному. Наоборот, хозяйство № 9 получило по 26,7 ц вместо расчетных 35,6 ц. Следовательно, эффективность использования средств на производство молока в этом хозяйстве (1616 руб. на корову) составила только 26,7 : 35,7 = 75% средней по совокупности.
Оценка хозяйственной деятельности по отклонениям от расчетных значений показателей на основе уравнений регрессии (тем более на основе многофакторных регрессионных моделей) гораздо более оправдана и содержательна, чем оценка результатов производства по отклонениям от среднего значения результативного признака в совокупности без учета факторов - характеристик возможностей и природных условий предприятия.
Уравнения регрессии применимо и для прогнозирования возможных ожидаемых значений результативного признака. При этом следует учесть, что перенос закономерности связи, измеренной в варьирующей совокупности, в статике на динамику не является, строго говоря, корректным и требует проверки условий допустимости такого переноса (экстраполяции), что выходит за рамки статистики и может быть сделано только специалистом, хорошо знающим объект (систему) и возможности его развития в будущем.
Ограничением прогнозирования на основании регрессионного уравнения, тем более парного, служит условие стабильности или по крайней мере малой изменчивости других факторов и условий изучаемого процесса, не связанных с ними. Если резко изменится "внешняя среда" протекающего процесса, прежнее уравнение регрессии результативного признака на факторный потеряет свое значение. В сильно засушливый год доза удобрений может не оказать влияния на урожайность сельскохозяйственной культуры, так как последнюю лимитирует недостаточная влагообеспеченность.
Прогнозируемое значение результативного показателя получается при подстановке в уравнение регрессии ожидаемой величины факторного признака. Так, если подставить в уравнение (8.14) расход средств на корову, равный 2200 руб., то получим ожидаемый надой молока от коровы, равный 55,85 ц. При таком прогнозировании следует соблюдать еще одно ограничение: нельзя подставлять значения факторного признака, значительно отличающиеся от входящих в базисную информацию, по которой вычислено уравнение регрессии. При качественно иных уровнях фактора, если они даже возможны в принципе, были бы другими параметры уравнения.
Можно рекомендовать при определении значений факторов не выходить за пределы трети размаха вариации как за минимальное, так и за максимальное значение признака-фактора, имевшееся в исходной информации.
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его значением средней ошибки прогноза или доверительным интервалам прогноза с достаточно большой вероятностью. Средняя ошибка положения линии регрессии в генеральной совокупности при значении факторного признака, равном хk, вычисляется для линии регрессии по формуле (8.20)
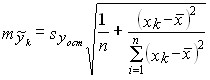 , (8.20) , (8.20)
где тy?k - средняя ошибка положения линии регрессии в генеральной совокупности при х = хk,
п - объем выборки;
хk - ожидаемое значение фактора;
syост - оценка среднего квадратического отклонения результативного признака от линии регрессии в генеральной совокупности с учетом степеней свободы вариации.
По данным табл. 8.1 находим syост .
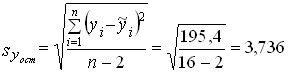 ц на одну корову ц на одну корову
При хл = 2200 руб. на 1 голову имеем:
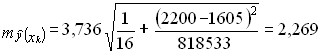 ц на 1 корову. ц на 1 корову.
Для вычисления доверительных границ прогноза линии регрессии нужно умножить ее среднюю ошибку на t-критерий Стьюдента. При 14 степенях свободы и доверительной вероятности 0,95 (α = 0,05) значение t-критерия равно 2,14. Получаем доверительные границы:
55,85 ± 2,629·2,14, или от 50,22 до 61,48 ц от 1 коровы. Интервал довольно широкий. Значительная неопределенность прогноза линии регрессии связана с малым объемом выборки. При объеме совокупности, равном 400, и той же вариации надоев ошибка прогноза была бы в 5 раз меньше и доверительный интервал был бы уже.
Средняя ошибка прогноза для индивидуального значения по правилу о дисперсии суммы независимых переменных образуется из ошибки прогноза положения линии регрессии и среднего квадратического отклонения индивидуальных значений от линии регрессии (остаточной вариации), т. е.
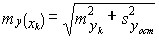 . (8.21) . (8.21)
В нашем примере имеем:
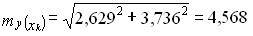 ц на 1 корову. ц на 1 корову.
Доверительные границы прогноза индивидуальных значений надоя молока на корову при расходе 2200 руб. на 1 голову составляют с вероятностью нахождения внутри границ, равной 0,95:
55,85 ± 4,568·2,14, или от 46,07 до 65,63 ц.
Главным источником ошибки неопределенности прогноза индивидуальных значений служит не столько неопределенность прогноза линии регрессии, сколько значительная вариация надоев за счет других факторов, кроме входящих в уравнение регрессии.
|