6.3. Многомерные группировки
Мы убедились, как трудно выбрать какой-то один признак в качестве основания группировки. Еще труднее проводить группировку по нескольким признакам. Комбинация двух признаков позволяет сохранить обозримость таблицы, но комбинация трех или четырех признаков дает совершенно неудовлетворительный результат: ведь даже при выделении трех категорий по каждому из груп-пировочных признаков мы получим 9 или 12 подгрупп. Равномерность распределения единиц по группам в принципе невозможна. Вот и получаются группы, в которые входят 1-2 наблюдения. Сохранить сложность описания групп и вместе с тем преодолеть недостатки комбинационной группировки позволяют методы многомерных группировок. Часто их называют методами многомерной классификации.
Эти методы получили распространение благодаря использованию |ЭВМ и пакетов прикладных программ. Цель этих методов — классификация данных, иначе говоря, группировка на основе множества |Признаков. Такие задачи широко распространены в науках о приро-|де и обществе, в практической деятельности по управлению массо-^Яыми процессами. Например, выделение типов предприятий по Ижнансовому положению, по экономической эффективности деятельности производится на основе множества признаков: выделение и изучение типов людей по степени их пригодности к определенной профессии (профпригодность); диагностика болезней на основании множества объективных признаков (симптомов) и т. д.
Простейшим вариантом многомерной классификации является группировка на основе многомерных средних.
Многомерной средней называется средняя величина нескольких признаков для одной единицы совокупности. Поскольку нельзя рассчитать среднюю величину абсолютных значений разных признаков выраженных в разных единицах измерения, то многомерная средняя вычисляется из относительных величин, как правило, - из отношений значений признаков для единицы совокупности к средним значениям этих признаков:
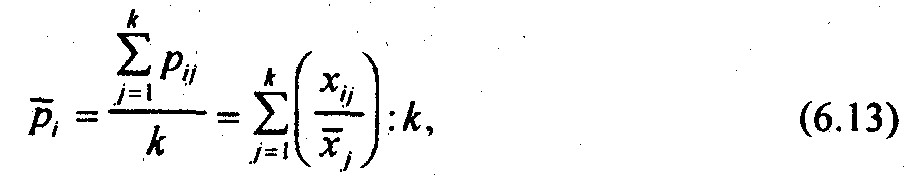
где p?j - многомерная средняя для i-единицы;
хij - значение признака х, для г-единицы;
хj - среднее значение признака xi,
k - число признаков;
j - номер признака;
i - номер единицы совокупности.
Рассмотрим использование многомерных средних на примере сельскохозяйственных предприятий Всеволожского района Ленинградской области за 1995 г. (табл. 6.8). По каждому предприятию приведены четыре признака:
• среднемесячная оплата труда работника, руб., x1;
• валовой доход на 1 га сельхозугодий, тыс. руб./га, х2;
• среднегодовая стоимость основных производственных фондов на 1 га сельхозугодий, млн руб./га, x3;
• отношение дебиторской задолженности к кредиторской задолженности, %, x4.
Эти признаки можно считать однородными, так как большая их величина положительно характеризует экономику предприятия. Предпочтительнее обобщать в многомерной средней признаки либо «положительные», либо «отрицательные» (чем больше, тем хуже).
Многомерные средние, приведенные в последней графе табл. 6.8, обобщают четыре признака.. При этом значимость признаков для оценки предприятия полагается одинаковой, что, конечно, спорно. Можно .усложнить методику, приписав признакам, на основе экспертнои оценки, разные веса, и вычислить взвешенные многомерные средние.
Таблица 6.8
Характеристики предприятий Всеволожского района Ленинградской области в 1995 г.
|
Предприятия
|
Значения признаков
|
В % к средней
|
Многомер-ная средняя, %
|
|
х1
|
х2
|
х3
|
х4
|
х1
|
х2
|
х3
|
х4
|
|
«Ручьи»
|
597
|
390
|
20,6
|
72
|
148
|
199
|
106
|
107
|
140
|
|
«Бугры»
|
353
|
96
|
12,1
|
30
|
88
|
49
|
62
|
45
|
61
|
|
«Пригородное»
|
403
|
84
|
20,6
|
26
|
100
|
43
|
106
|
39
|
72
|
|
«Авлога»
|
231
|
71
|
15,1
|
74
|
57
|
36
|
78
|
110
|
70
|
|
«Всеволожское»
|
330
|
114
|
14,8
|
159
|
82
|
58
|
76
|
237
|
113
|
|
«Выборгское»
|
540
|
235
|
24,0
|
26
|
134
|
120
|
184
|
39
|
104
|
|
«Приневское»
|
372
|
461
|
33,2
|
85
|
93
|
235
|
171
|
127
|
156
|
|
«Шеглово»
|
393
|
113
|
15,0
|
62
|
98
|
58
|
77
|
92
|
81
|
|
Средние величины
|
402
|
196
|
19,4
|
67
|
100
|
100
|
100
|
100
|
100
|
|
Средние квадратические отклонения
|
109
|
142
|
6,4
|
41
|
-
|
-
|
-
|
-
|
-
|
Судя по полученным оценкам, предприятия делятся на группы с многомерными средними ниже 100% (четыре предприятия), несколько выше 100% (два предприятия) и резко превышающие 100% (два предприятия).
При большом 'объеме совокупности для выделения групп на основе многомерной средней необходимо установить интервалы значений многомерной средней;
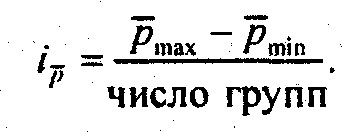
Затем следует провести группировку единиц: определить их количество в каждой группе и постараться указать, в чем состоят качественные различия между группами.
Более обоснованным методом многомерной классификации является кластерный анализ. Само название метода происходит от того же корня, что и слово «класс», «классификация». Английское слово the cluster имеет значения: группа, пучок, куст, т. е. объединений каких-то однородных явлений. В данном контексте оно близко к математическому понятию «множества», причем, как и множество, кластер может содержать только одно явление, но не может в отличие от множества быть пустым.
Каждая единица совокупности в кластерном анализе рассматривается как точка в заданном признаковом пространстве. Значение каждого из признаков у данной единицы служит ее координатой в этом «пространстве» по аналогии с координатами точки в нашем реальном трехмерном пространстве. Таким образом, признаковое пространство - это область варьирования всех признаков совокупности изучаемых явлений. Если мы уподобим это пространство обычному пространству, имеющему евклидову метрику, то тем самым мы получим возможность измерять «расстояния» между точками признакового пространства. Эти расстояния называют евклидовыми. Их вычисляют по тем же правилам, как и в обычной евклидовой геометрии. На плоскости, т.е. в двухмерном пространстве, расстояние между точками А и В равно корню квадратному из суммы квадратов разностей координат этих точек по оси абсцисс и по оси ординат - на основании теоремы Пифагора (рис. 6.1).
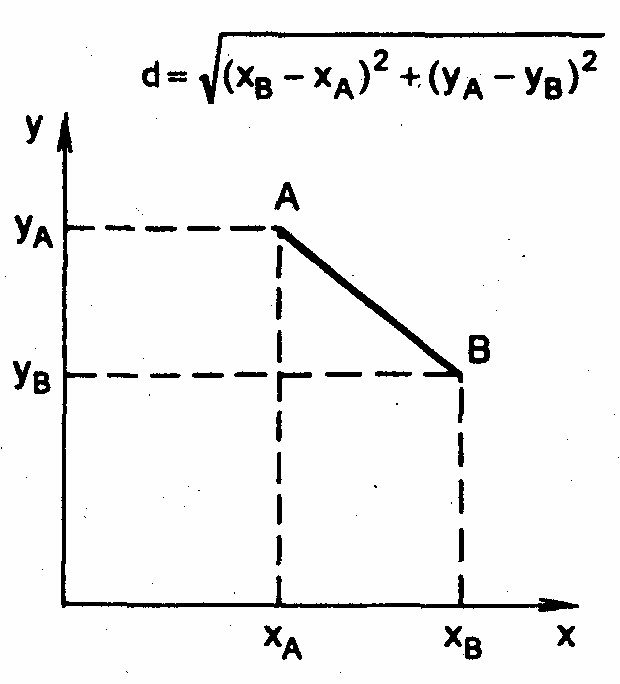
Рис. 6.1. Евклидово расстояние
В многомерном признаковом пространстве расстояние между точками р и q с k координатами, т. е. индивидуальными значениями k признаков, определяется так:
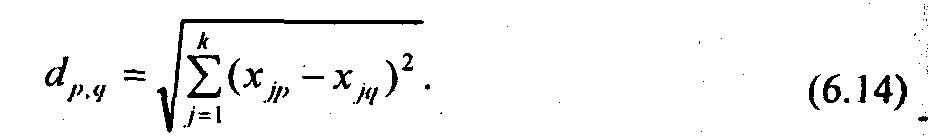
Совершенно очевидно, что нельзя суммировать квадраты отклонений одной точки от другой в абсолютных значениях разнокачествен-ных признаков. Необходимо сначала выразить различия между единицами совокупности по каждому признаку в каком-то относитель,но безразмерном показателе. В качестве такого показателя часто применяют «нормированную разность», т. е. величину:


По данным табл. 6.8 среднее квадратическое отклонение признака х, равно 109. Разделив все попарные разности значений этого признака на 109, получим матрицу нормированных разностей D1 (табл. 6.9). Очевидно эта матрица размером п?п симметрична.
Таблица 6.9
Матрица нормированных разностей между предприятиями по
среднемесячной оплате труда (D1)
|
Предприятия
|
«Ручьи»
|
«Бугры»
|
«Пригородное»
|
«Авлога»
|
«Все-волож-ское»
|
«Вы-борг-ское»
|
«При-нев-ское»
|
«Щег-лово»
|
|
«Ручьи»
|
0
|
|
|
|
|
|
|
|
|
«Бугры»
|
2,239
|
0
|
|
|
|
|
|
|
|
«Пригородное»
|
1,780
|
0,459
|
0
|
|
|
|
|
|
|
«Авлога»
|
3,358
|
1,119
|
1,578
|
0
|
|
|
|
|
|
«Всеволожское»
|
2,450
|
0,211
|
0,670
|
0,908
|
0
|
|
|
|
|
«Выборгское»
|
0,523
|
1,716
|
1,257
|
2,835
|
1,927
|
0
|
|
|
|
«Приневское»
|
2,064
|
0,174
|
0,284
|
1,294
|
0,385
|
1,541
|
0
|
|
|
«Щеглово»
|
1,872
|
0,367
|
0,092
|
1,486
|
0,518
|
1,349
|
0,193
|
0
|
Из данных табл. 6.9 видно, что величина нормированных разностей по этому признаку варьирует от 0 до 3,4. В нормально распределенной совокупности различия признака в среднем лишь в трех случаях из тысячи превосходят шесть сигм, т. е. в распределениях, близких к нормальным, величина нормированного расстояния редко превосходит 6.
Средняя нормированная разность по данным табл. 6.9 составила 1,182. В нормально распределенной совокупности и совпадает со средним отклонением их от средней величины, т.е. нормированная разность в нормальной совокупности в среднем равна единице. Это очень важно при установлении предельного (критического) расстояния в признаковом пространстве, при достижении которого прекращается объединение кластеров.
Аналогично вычисляются матрицы нормированных разностей по признакам х2, х3, х4 (см. табл. 6.10-6.12).
Таблица 6.10
Матрица нормированных разностей между предприятиями
по валовому доходу на 1 га сельхозугодий D2)
|
Предприятия
|
«Ручьи»
|
«Бугры»
|
«Пригородное»
|
«Авлога»
|
«Все-волож-ское»
|
«Вы-борг-ское»
|
«При-нев-ское»
|
«Щеглово»
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
«Ручьи»
|
0
|
|
|
|
|
|
|
|
|
«Бугры»
|
2,070
|
0
|
|
|
|
|
|
|
|
«Пригородное»
|
2,155
|
0,085
|
0
|
|
|
|
|
|
Продолжение таблицы 6.10
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
«Авлога»
|
2,246
|
0,176
|
0,092
|
0
|
|
|
|
|
|
«Всеволожское»
|
1,944
|
0,127
|
0,211
|
0,303
|
0
|
|
|
|
|
«Выборгское»
|
1,092
|
0,972
|
1,063
|
1,155
|
0,852
|
0
|
|
|
|
«Приневское»
|
0,500
|
2,552
|
2,636
|
2,746
|
2,444
|
1,592
|
0
|
|
|
«Щеглово»
|
1,951
|
0,119
|
0,203
|
0,296
|
0,007
|
0,859
|
2,451
|
0
|
Таблица 6.11
Матрица нормированных разностей между предприятиями по
среднегодовой стоимости основных производственных фондов на 1 га
сельхозугодий (D3)
|
Предприятия
|
«Ручьи»
|
«Бугры»
|
«Пригородное»
|
«Авлога»
|
«Все-волож-ское»
|
«Вы-борг-ское»
|
«При-нев-ское»
|
«Щеглово»
|
|
«Ручьи»
|
0
|
|
|
|
|
|
|
|
|
«Бугры»
|
1,328
|
0
|
|
|
|
|
|
|
|
«Пригородное»
|
0
|
1,328
|
0
|
|
|
|
|
|
|
«Авлога»
|
0,859
|
0,469
|
0,859
|
0
|
|
|
|
|
|
«Всеволожское»
|
0,906
|
0,422
|
0,906
|
0,047
|
0
|
|
|
|
|
«Выборгское»
|
0,531
|
1,859
|
0,531
|
1,39.1
|
1,438
|
0
|
|
|
|
«Приневское»
|
1,969
|
3,297
|
1,906
|
2,828
|
2,875
|
1,438
|
0
|
|
|
«Щеглово»
|
0,875
|
0,453
|
0,875
|
0,016
|
0,031
|
1,406
|
2,844
|
0
|
Средняя нормированная разность d?3 = 1,11.
Таблица 6.12
Матрица нормированных разностей между предприятиями ю
отношению дебиторской задолженности к кредиторской (D4)
|
Предприятия
|
«Ручьи»
|
«Бугры»
|
«Пригородное»
|
«Авлога»
|
«Все-волож-ское»
|
«Вы-борг-ское»
|
«При-нев-екое»
|
«Щеглово»
|
|
«Ручьи»
|
0
|
|
|
|
|
|
|
|
|
«Бугры»
|
1,024
|
0
|
|
|
|
|
|
|
|
«Пригородное»
|
1,122
|
0,098
|
0
|
|
|
|
|
|
|
«Авлога»
|
0,049
|
1,073
|
1,171
|
0
|
|
|
|
|
|
«Всеволож-ское»
|
2,122
|
3,146
|
3,244
|
2,073
|
0
|
|
|
|
|
«Выборг-ское»
|
1,122
|
0,098
|
0
|
1,171
|
3,244
|
0
|
|
|
|
«Принев-ское»
|
0,317
|
1,341
|
1,439
|
0,268
|
1,805
|
1,439
|
0
|
|
|
«Щеглово»
|
0,244
|
0,780
|
0,878
|
0,293
|
2,366
|
0,878
|
0,561
|
0
|
Средняя нормированная разность d?4 = 1,086.
На основе данных таблиц 6.9 - 6.12 формируется матрица евклидовых расстояний D (табл. 6.13).
С учетом нормировки разности признаков расстояние между двумя любыми единицами совокупности (точками в признаковом пространстве) имеет вид:

Например, расстояние между предприятиями «Ручьи» и «Бугры», согласно формуле (6.16), составляет:
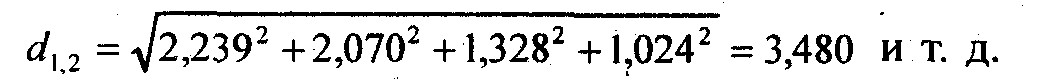
Таблица 6.13
Матрица нормализованных (нормированных) евклидовых
расстояний (D)
|
Предприятия
|
«Ручьи»
|
«Бугры»
|
«Пригородное»
|
«Авлога»
|
«Все-волож-ское»
|
«Вы-борг-ское»
|
«При-нев-ское»
|
«Щеглове»
|
|
«Ручьи»
|
0
|
|
|
|
|
|
|
|
|
«Бугры»
|
3,480
|
0
|
|
|
|
|
|
|
|
«Пригородное»
|
3,012
|
1,411
|
0
|
|
|
|
|
|
|
«Авлога»
|
4,130
|
1,629
|
2,885
|
0
|
|
|
|
|
|
«Всеволожское»
|
3,887
|
3,184
|
3,441
|
2,284
|
0
|
|
|
|
|
«Выборгское»
|
1,734
|
2,712
|
1,373
|
3,559
|
4,127
|
0
|
|
|
|
«Приневское»
|
2,913
|
4,383
|
3,568
|
4,157
|
4,188
|
3,008
|
0
|
|
|
«Щеглове»
|
2,852
|
0,981
|
1,130
|
1,541
|
2,422
|
2,281
|
3,775
|
0
|
Матрица евклидовых расстояний D служит основой агломеративно-иерархического метода классификации, который заключается в последовательном объединении группируемых объектов -сначала самых близких, а затем все более удаленных друг от друга. Процедура классификации состоит из последовательных шагов, на каждом из которых производится объединение двух ближайших групп объектов (кластеров). На нулевом шаге каждый объект рассматривается как отдельный кластер. На первом шаге объединим в кластер предприятия с наименьшим евклидовым расстоянием («Бугры» и «Щеглове»). Найдем средние по всем признакам для этого кластера и евклидовы расстояния от кластера до других предприятий (табл. 6.14).
Таблица 6.14
Нормированные разности и евклидовы расстояния для кластера «Бугры + Щеглово»
|
Предприятия
|
|
Признаки
|
Евклидово расстояние
|
|
х1
|
х2
|
х3
|
х4
|
|
Средние величины
|
|
|
|
|
|
|
по кластеру
|
373
|
104,5
|
13,55
|
46
|
-
|
|
«Ручьи»
|
2,055
|
2,011
|
1,094
|
0,634
|
3,141
|
|
«Пригородное»
|
0,275
|
0,144
|
1,094
|
0,488
|
1,237
|
|
«Авлога»
|
1,303
|
0,236
|
0,242
|
0,683
|
1,509
|
|
«Всеволожское»
|
0,394
|
0,667
|
0,195
|
2,756
|
2,869
|
|
«Выборгское»
|
1,532
|
0,919
|
1,633
|
0,488
|
2,469
|
|
«Приневское»
|
0,003
|
2,511
|
3,070
|
0,951
|
4,079
|
Заменив в матрице евклидовых расстояний (табл. 6.13) расстояния предприятий, вошедших в первый кластер, на числа последней графы табл. 6.14, видим, что теперь минимальным является расстояние между предприятием «Пригородное» и первым кластером: d= 1,237 (табл. 6.15).
Следовательно, на втором шаге к первому кластеру присоединяется предприятие «Пригородное». Вычисляем средние величины, нормированные разности по каждому признаку и евклидовы расстояния от кластера, включающего три предприятия («Бугры», «Щеглове», «Пригородное») до каждого из оставшихся предприятий. Результаты представлены в табл. 6.16.
Заменив евклидовы расстояния предприятий, вошедших в кластер, данными последней графы табл. 6.16, получим новую матрицу евклидовых расстояний (табл. 6.17).
Минимальным является евклидово расстояние от кластера до предприятия «Авлога». На третьем шаге образуем кластер «Бугры + Щеглове + Пригородное + Авлога». Полученные средние величины для кластера, нормированные разности и евклидовы расстояния представлены в табл. 6.18, 6.19.
Таблица 6.15
Матрица евклидовых расстояний после образования кластера
«Бугры + Щеглове»
|
Предприятия
|
«Бугры + Щеглово»
|
«Ручьи»
|
«Пригородное»
|
«Авлога»
|
«Всево-лож-ское»
|
«Вы-боргс-кое»
|
«При-нев-ское»
|
|
Кластер «Бугры + Щеглово»
|
0
|
|
|
|
|
|
|
|
«Ручьи»
|
3,141
|
0
|
|
|
|
|
|
|
«Пригородное»
|
1,237
|
3,012
|
0
|
|
|
|
|
|
«Авлога»
|
1,509
|
4,130
|
2,885
|
0
|
|
|
|
|
«Всеволожское»
|
2,869
|
3,887
|
3,441
|
2,284
|
0
|
|
|
|
«Выборгское»
|
2,469
|
1,734
|
1,731
|
3,559
|
4,127
|
0
|
|
|
«Приневское»
|
4,079
|
2,913
|
3,568
|
4,157
|
4,183
|
3,008
|
0
|
Таблица 6.16
Нормированные разности и евклидовы расстояния для кластера «Бугры + Щеглове + Пригородное»
|
Предприятия
|
Признаки
|
Евклидово расстояние
|
|
х1
|
х2
|
х3
|
х4
|
|
Средние величины по кластеру
|
383
|
98
|
15,9
|
39
|
0
|
|
«Ручьи»
|
1,963
|
2,056
|
0,734
|
0,805
|
3,044
|
|
«Авлога»
|
1.394
|
0,190
|
0,125
|
0,854
|
1,651
|
|
«Всеволожское»
|
0,486
|
0,113
|
0,172
|
2,927
|
2,974
|
|
«Выборгское»
|
1,440
|
0,965
|
1,266
|
0,317
|
2,170
|
|
«Приневское»
|
0,101
|
2,556
|
2,703
|
1,122
|
3,887
|
Таблица 6.17
Матрица евклидовых расстояний после образования кластера
«Бугры + Щеглово + Пригородное»
|
Предприятия
|
Кластер Б+Щ+П
|
«Ручьи»
|
«Авлога»
|
«Всеволожское»
|
«Выборгское»
|
«Приневское»
|
|
Кластер Б+Щ+П
|
0
|
|
|
|
|
|
|
«Ручьи»
|
3,044
|
0
|
|
|
|
|
|
«Авлога»
|
1,651
|
4,130
|
0
|
|
|
|
|
«Всеволожское»
|
2,974
|
3,887
|
2,884
|
0
|
|
|
|
«Выборгское»
|
2,170
|
1,734
|
3,559
|
4,127
|
0
|
|
|
«Приневское»
|
3,887
|
2,913
|
4,157
|
4,188
|
3,008
|
0
|
Таблица 6.18
Нормированные разности и евклидовы расстояния для кластера «Бугры + Щеглово + Пригородное + Авлога»
|
Предприятия
|
|
Признаки
|
Евклидово расстояние
|
|
х1
|
х12
|
х3
|
х4
|
|
Средние величины по кластеру
|
345
|
91
|
15,7
|
48
|
0
|
|
«Ручьи»
|
2,312
|
2,106
|
0,766
|
0,585
|
3,273 .
|
|
«Всеволожское»
|
0,138
|
0,162
|
0,141
|
2,707
|
2,719
|
|
«Выборгское»
|
1,789
|
1,014
|
1,297
|
0,537
|
2,490
|
|
«Приневское»
|
0,248
|
2,606
|
2,734
|
0,902
|
3,891
|
Таблица 6.19
Матрица евклидовых расстояний после образования кластера
«Бугры + Щеглове + Пригородное + Авлога»
|
Предприятия
|
Кластер Б+Щ+П+А
|
«Ручьи»
|
«Всеволож-ское»
|
«Выборгское»
|
«Приневское»
|
|
Кластер Б+Щ+П+А
|
0
|
|
|
|
|
|
«Ручьи»
|
3,273
|
0
|
|
|
|
|
«Всеволожское»
|
2,719
|
3,887
|
0
|
|
|
|
«Выборгское»
|
2,490
|
1,734
|
4,127
|
0
|
|
|
«Приневское»
|
3,891
|
2,913
|
4,188
|
3,008
|
0
|
Минимальное евклидово расстояние между предприятиями «Ручьи - Выборгское» (оно меньше 2), следовательно, эти предприятия объединяются в кластер 2 (табл. 6.20). Кластер Б+Щ+П+А будем называть кластером 1.
Таблица 6.20
Нормированные разности и евклидовы расстояния для
кластеров 1 и 2
|
Предприятия
|
Признаки
|
Евклидово расстояние
|
|
х1
|
х2
|
х3
|
х4
|
|
Средние кластера 2
|
568
|
312
|
22,3
|
49
|
0
|
|
Кластер 1
|
2,046
|
1,556
|
1,031
|
0,024
|
2,770
|
|
«Всеволожское»
|
2,183
|
1,394
|
1,172
|
2,683
|
3,904
|
|
«Приневское»
|
1,798
|
1,049
|
1,703
|
0,878
|
2,829
|
После четвертого шага получаем новую матрицу евклидовых расстояний (табл. 6.21).
Согласно табл. 6.21 все расстояния больше 2. Оставляем 4 типа предприятий: предприятия, вошедшие в кластер 1, кластер 2, кластер 3 («Всеволожское») и кластер 4 («Приневское»).
Сравнивая результат кластерного анализа с многомерными средними (табл. 6.8) видим, что состав кластера 1 точно отвечает тем хозяйствам, чьи многомерные средние ниже 100%. Также выделение в самостоятельный кластер предприятия «Приневское» соответствует его высшему значению многомерной средней. А вот объединение в кластер 2 предприятий «Ручьи» и «Выборгское» не соответствует многомерным средним, по которым к предприятию «Ручьи» было ближе предприятие «Всеволожское». В результате резкого отличия по признаку х4 предприятие «Всеволожское» выделилось в отдельный кластер 3.
Таблица 6.21
Матрица евклидовых расстояний после образования кластера 2
|
|
Кластер 1
|
Кластер 2
|
Кластер 3 («Всеволожское»)
|
Кластер 4 («Приневское»)
|
|
Кластер 1
|
0
|
|
|
|
|
Кластер 2
|
2,770
|
0
|
|
|
|
«Всеволожское»
|
2,719
|
3,909
|
0
|
|
|
«Приневское»
|
3,891
|
2,829
|
4,188
|
0
|
Обобщая рассмотренную процедуру кластерного анализа, представим действия в виде определенной последовательности:
1) вычисление средних величин каждого из классификационных признаков х?j в целом по совокупности;
2) вычисление средних квадратических отклонений каждого из признаков по совокупности – sxj или ?xj,
3) вычисление матриц нормированных разностей по каждому из группировочных признаков – djp,q;
4) вычисление евклидовых расстояний между каждой парой сочетаний единиц совокупности – dp,q;
5) выбор наименьшего из евклидовых расстояний – dp,qmin;
6) объединение единиц совокупности с наименьшим евклидовым расстоянием между ними в один кластер;
7) вычисление средних значений всех признаков для единиц, объединенных в кластер;
8) вычисление новых нормированных расстояний между объединенным кластером и остальными единицами;
9) вычисление новых евклидовых расстояний между объединенным кластером и остальными единицами (или кластерами);
10) выбор наименьшего из евклидовых расстояний;
11) повторение операций (6-10) и т.д.
Объединение в кластеры прекращается, когда все евклидовы расстояния превысят заданную критическую величину dкрит. Обычно ППП предусматривает вывод на печать состава (перечня единиц совокупности) каждого кластера, евклидовых расстояний между ними, матриц нормированных разностей по каждому признаку.
Существует много достаточно сложных алгоритмов кластерного анализа и родственных ему методов распознавания образов, таксономии и др.
Рассмотренная выше методика вычисления евклидова расстояния предполагает, что все признаки считаются равноправными. На самом же деле при выделении типов социально-экономических явлений группировочные признаки не равноправны: как правило, одни признаки имеют большее, другие — меньшее значение. Следовательно, более совершенная методика кластерного анализа должна учитывать разную значимость, разный «вес» группировочных признаков. В этом случае должно использоваться взвешенное евклидово расстояние:
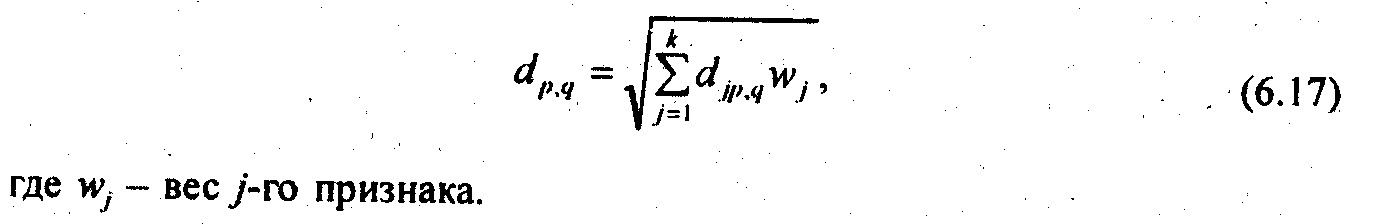
Определение весов - весьма сложная задача, выходящая за пределы компетенции статистики. О том, какие признаки важнее при классификации тех или иных объектов, могут судить не статистики, а специалисты в соответствующей отрасли. Поэтому одним из способов определения весов признаков при кластерном анализе являются экспертные оценки. Опросив достаточное число специалистов-экспертов (желательно не менее 6-10), статистик сможет определить по их оценкам места (роли) каждого группировочного признака. Затем находится среднее по оценкам всех экспертов место признака или его «вес» в численном выражении. Можно просить экспертов ранжировать признаки по порядку значимости и определять «среднее место», но оценка при этом будет очень грубая: признак, поставленный на первое место, будет вдвое важнее второго и в двадцать или тридцать раз важнее последнего. Чтобы различия весов были не столь резкими, можно просить экспертов распределить между группировочными признаками, в соответствии с их значениями, общую сумму оценок (100 или 1000%). Тогда каждому из признаков будет приписана некоторая доля этой общей суммы, можно двум-трем признакам приписать одинаковые веса. Но этот способ взвешивания требует от экспертов большей точности и напряжения, чем простое ранжирование признаков.
Субъективность экспертных оценок в какой-то мере можно компенсировать статистической обработкой. Например, по каждому признаку перед определением средней оценки его веса можно отбросить максимальную и минимальную оценки, если они резко отличаются от оценок остальных экспертов. Можно вообще исключить того эксперта, чьи оценки в среднем отличаются от средних оценок признаков более чем, например, на 2?. Однако эти статистические коррективы небезупречны и допустимы при значительном числе экспертов для того, чтобы их средние оценки были надежны.
Существует и другая возможность оценки роли группировочных признаков, их значимости для классификации: на основе стандартизованных коэффициентов регрессии или коэффициентов раздельной детерминации (см. гл. 8).
Рассмотренный алгоритм иерархической классификации можно модифицировать, используя метод «ближайшего» или «дальнего соседа» (табл. 6.22). В этом случае в матрицу евклидовых расстояний вводятся расстояния, полученные не на основе средних величин по кластеру, в качестве представителя кластера берется входящий в него объект либо наименее удаленный от остальных объектов («ближайший сосед»), либо наиболее удаленный от остальных («дальний сосед»). Поскольку </„,„ = 0,981 (табл. 6.13) предприятия «Бугры» и «Щеглове» были объединены в кластер. При использовании метода «ближайшего соседа» в последующей после объединения этих двух предприятий матрице евклидовых расстояний кластер будет представлять то «Бугры», то «Щеглове» - в зависимости от того, какое из предприятий наименее удалено от остальных. Для простоты будем использовать не названия, а порядковые номера предприятий, соответствующие их последовательности в табл. 6.8.
Таблица 6.22
Матрица евклидовых расстояний на первом шаге
(метод «ближайшего соседа»)
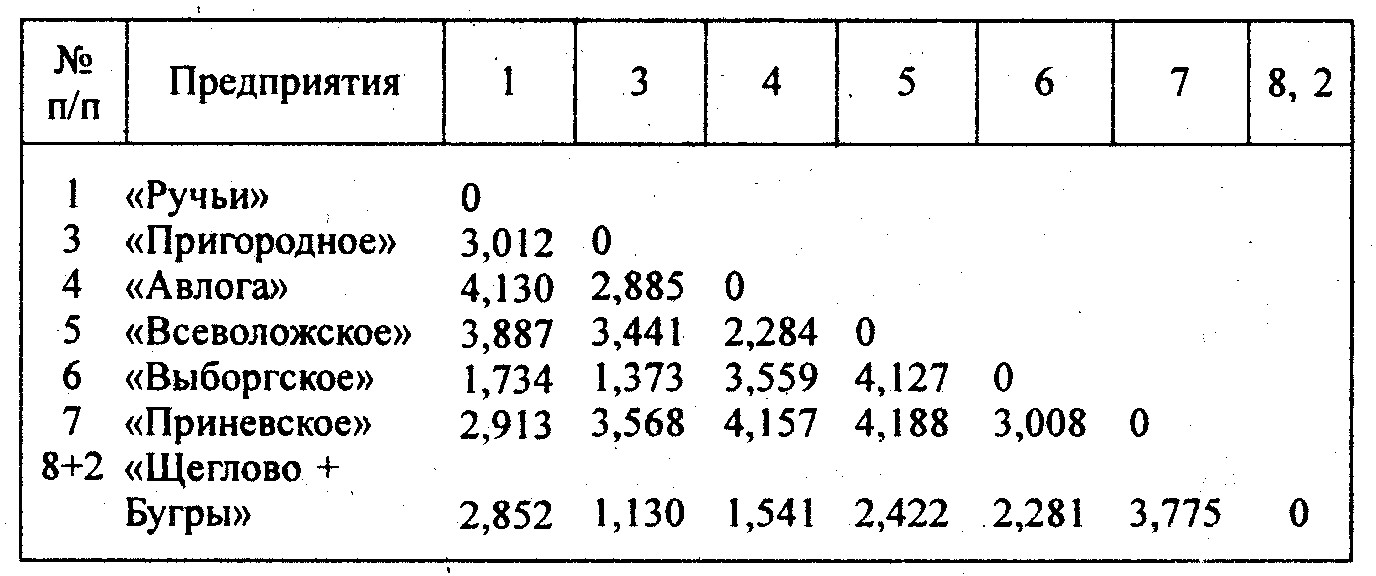
Минимальное евклидово расстояние между кластером и предприятием «Пригородное» d8,2,3 = 1,130. (табл. 6.13). Это хозяйство имеет номер 3, присоединим его к кластеру (8.2). Матрица евклидовых расстояний на втором шаге будет следующей (табл. 6.23).
Таблица 6.23
Матрица евклидовых расстояний на втором шаге
(метод «ближайшего соседа»)
|
Предприятия
|
1
|
4
|
5
|
6
|
7
|
8,2, 3
|
|
1
|
0
|
|
|
|
|
|
|
4
|
4,130
|
0
|
|
|
|
|
|
5
|
3.887
|
2,284
|
0
|
|
|
|
|
6
|
1,734
|
3,559
|
4,127
|
0
|
|
|
|
7
|
2,913
|
4,157
|
4,188
|
3,008
|
0
|
|
|
8, 2, 3
|
2,852
|
1,541
|
2,422
|
1,373
|
3.568
|
0
|
Минимальным является расстояние между предприятием («Вы-боргское») и кластером: min d8,2,3,6 = 1,373. При кластере из четырех предприятий матрица евклидовых расстояний представлена в табл. 6.24.
Таблица 6.24
Матрица евклидовых расстояний на третьем шаге
(метод «ближайшего соседа»)
|
Предприятия
|
1
|
4
|
5
|
7
|
8, 2, 3, 6
|
|
1
|
0
|
|
|
|
|
|
4
|
4,130
|
0
|
|
|
|
|
5
|
3,887
|
2,284
|
0
|
|
|
|
7
|
2,913
|
4,157
|
4,188
|
0
|
|
|
8, 2, 3, 6
|
1,734
|
1,541
|
2,422
|
3,008
|
0
|
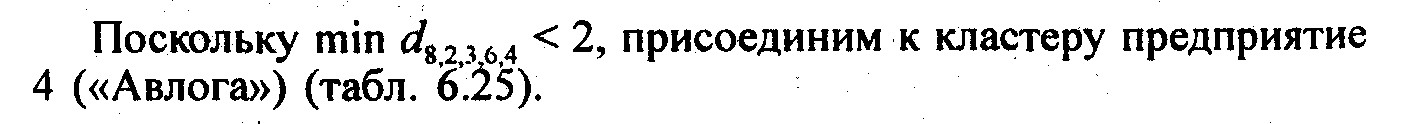
Таблица 6.25
Матрица евклидовых расстояний на четвертом шаге
(метод «ближайшего соседа»)
|
Предприятия
|
1
|
5
|
7
|
8, 2, 3, 6, 4
|
|
1
|
0
|
|
|
|
|
5
|
3,887
|
0
|
|
|
|
7
|
2,913
|
4,188
|
0
|
|
|
8, 2, 3, 6, 4
|
1,734
|
2,284
|
3,008
|
0
|
Сравнивая табл. 6.24 и 6.25, видим, что расстояния между кластером и объектом 1 и в обоих случаях определяются объектом 6, который является «ближайшим соседом» объекта 1. При определении расстояния между кластером и предприятием 7 представителем кластера выступает предприятие 6, которое является ближайшим к предприятию 7.
На следующем шаге к кластеру присоединяется предприятие 1 (6.26).
Таблица 6.26
Матрица евклидовых расстояний на пятом шаге
(метод «ближайшего соседа»)
|
Предприятия
|
5
|
7
|
8, 2. 3. 6, 4, 1
|
|
5
|
0
|
|
|
|
7
|
4,188
|
0
|
|
|
8,2,3,6,4,1
|
2,284
|
2,913
|
0
|
Расстояние между кластером и предприятием 5 также, как и на предыдущем шаге, определяется расстоянием между предприятиями 5 и 4, которое является ближайшим к 5 из всех предприятий, входящих в кластер. Расстояние между предприятием 7 и кластером в табл. 6.26 стало определяться «ближайшим соседом» - предприятием 1. Если продолжить процедуру классификации, то посколь-.ку минимальным расстоянием в табл. 6.26 является расстояние Цяежду кластером и предприятием 5, то можно присоединить его к ^кластеру (табл. 6.27).
Таблица 6.27
Евклидово расстояние на шестом шаге
|
Предприятия
|
7
|
8, 2, 3, 6, 4, 1, 5
|
|
7
|
0
|
|
|
8, 2, 3, 6, 4, 1, 5
|
2,913
|
0
|
В этом случае мы получим два кластера: один состоит из предприятия 7 («Приневское»), а другой включает остальные семь предприятий. Если придерживаться некоторого критического значения евклидовою расстояния так, как в ранее рассмотренном примере, когда d = 2, то предприятие 5 не присоединяется к кластеру и в итоге совокупность подразделяется на три кластера, два из которых содержат по одному предприятию (5 и 7) и один - шесть предприятий.
Представим графически процесс классификации в виде дендрограммы (рис. 6.2).
Дендрограмма - дерево объединений кластеров с порядковыми номерами объектов по горизонтальной оси и шкалой расстояний по вертикальной оси.
Решение, полученное методом «ближайшего соседа», близко к прежнему результату при описании кластеров средними показателями (табл. 6.21), но не совпадает с ним - вместо четырех кластеров здесь выделились три.
Таблица 6.28
Матрица евклидовых расстояний на первом шаге
(метод «дальнего соседа»)
|
Предприятия
|
1
|
3
|
4
|
5
|
6
|
7
|
8+2
|
|
1
|
0
|
|
|
|
|
|
|
|
3
|
3,012
|
0
|
|
|
|
|
|
|
4
|
4,130
|
.2,885
|
0
|
|
|
|
|
|
5
|
3,887
|
3,441
|
2,284
|
0
|
|
|
|
|
6
|
1,734
|
1,373
|
3,559
|
4,127
|
0
|
|
|
|
7
|
2,913
|
3,568
|
4,157
|
4,188
|
3,008
|
0
|
|
|
8+2
|
3,480
|
1,411
|
1,629
|
3,184
|
2,712
|
4,383
|
0
|

Рис. 6.2. Дендрограмма: метод «ближайшего соседа»
Если применить метод «дальнего соседа», то на первом шаге после объединения предприятий 2 и 8, получим следующую матрицу евклидовых расстояний (табл. 6.28). Табл. 6.28 отличается от табл. 6.21 последней строкой, в которой показаны максимальные расстояния кластера (8 + 2) от других объектов.
Затем выбирается наименьшее из dp,q . В данном примере это расстояние между хозяйствами 3 и 6 (d3,6 = 1,373),образующими новый кластер, в котором также выделяется «дальний сосед» (табл. 6.29).
Таблица 6.29
Матрица евклидовых расстояний на втором шаге
(метод «дальнего соседа»)
|
Предприятия
|
1
|
3+6
|
4
|
5
|
7
|
8+2
|
|
1
|
0
|
|
|
|
|
|
|
3+6
|
3,012
|
0
|
|
|
|
|
|
4
|
4,130
|
2,885
|
0
|
|
|
|
|
5
|
3,887
|
4,127
|
2,284
|
0
|
|
|
|
7
|
2,913
|
3,568
|
4,157
|
4,188
|
0
|
|
|
8+2
|
3,480
|
2,712
|
1,629
|
3,184
|
4,383
|
0
|
В табл. 6.29 dmin = d8+2,4 = 1,629. Таким образом, на третьем шаге к кластеру 8+2 присоединяется предприятие 4 (табл. 6.30).
Таблица 6.30
Матрица евклидовых расстояний на третьем шаге
(метод «дальнего соседа»)
|
Предприятия
|
1
|
3+6
|
5
|
7
|
8+2+4
|
|
1
|
0
|
|
|
|
|
|
3+6
|
3,012
|
0
|
|
|
|
|
5
|
3,887
|
4,127
|
0
|
|
|
|
7
|
2,913
|
3,568
|
4,188
|
0
|
|
|
8+2+4
|
4,130
|
3,559
|
3,184
|
4,383
|
0
|
В табл. 6.30 все значения dp,q > 2. Следовательно, в результате метода «дальнего соседа» получаем 5 кластеров, три из которых включают по одному предприятию.
Подведем итоги.
Все алгоритмы многомерной классификации основаны на целевой функции:
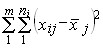 , ,
т. е. выделение однородных групп при минимизации внутригрупповой колеблемости.
Поиск однородных групп основан либо на измерении различия между объектами (так, как это было в рассмотренном примере), либо на измерении сходства между ними. Евклидово расстояние является одной из наиболее распространенных мер различия.
Любые функции расстояния (различия) между объектами d(Xi, Xj) обладают следующими свойствами:
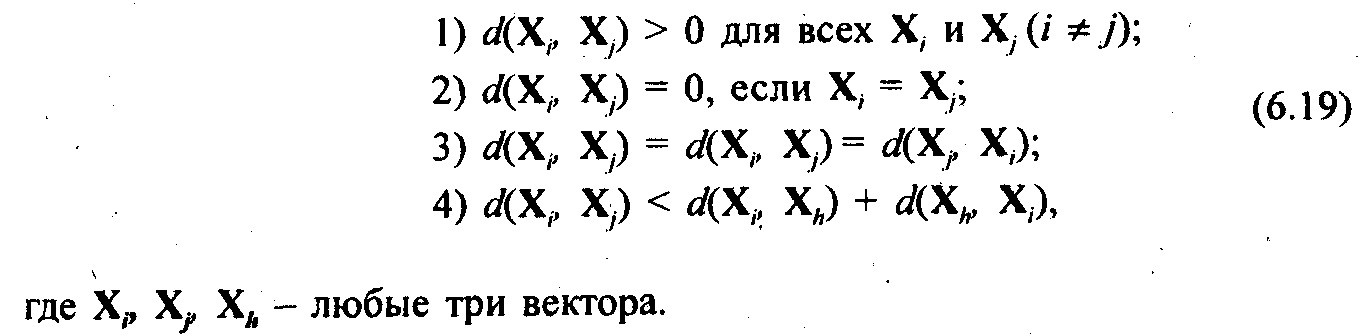
Расстояния между парами векторов d(Xi, Xj) могут быть представлены в виде симметричной матрицы расстояний:
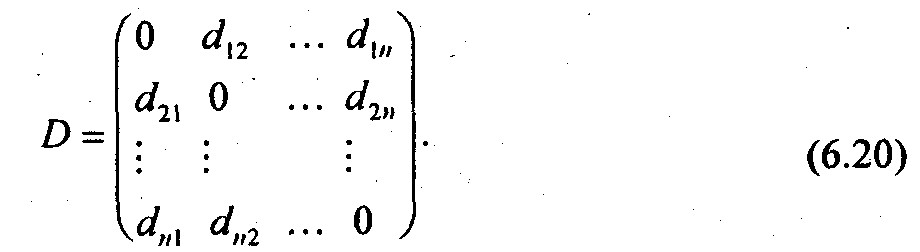
Диагональные элементы dii для всех i равны нулю. Расстояние между кластером i +j и всеми другими кластерами вычисляется в соответствии с выбранной стратегией классификации как
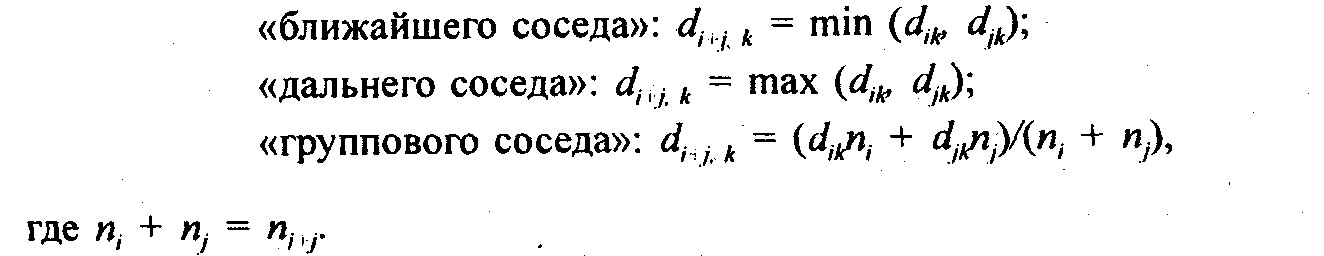
Метод «ближайшего соседа» сжимает пространство исходных переменных и рекомендуется для получения минимального дерева иерархической классификации. Метод «дальнего соседа» растягивает пространство. Метод «группового соседа» сохраняет метрику пространства.
Если классификация данных основана на мерах сходства s(X,, X,), то следует иметь в виду общие свойства этих мер:

Диагональные элементы такой матрицы равны 1.
В качестве мер сходства чаще всего используются коэффициенты корреляции (см. гл. 8).
Основными ППП для решения задачи многомерной классификации являются «Класс-мастер», SPSS, SAS. Многие алгоритмы многомерной классификации основаны на геометрическом представлении кластера как локального скопления точек в заданном признаковом пространстве.
Большинство методов классификации основано на однозначном отнесении объекта к тому или иному классу. Но, как уже отмечалось, границы классов могут быть размытыми, нечеткими. Класс объектов, в котором нет резкой границы между объектами, входящими в него, и теми, которые в него не входят, называется нечетким множеством.
Для классификации данных в нечетких множествах необходимо ввести матрицу принадлежности каждого объекта к нечеткому множеству с элементами
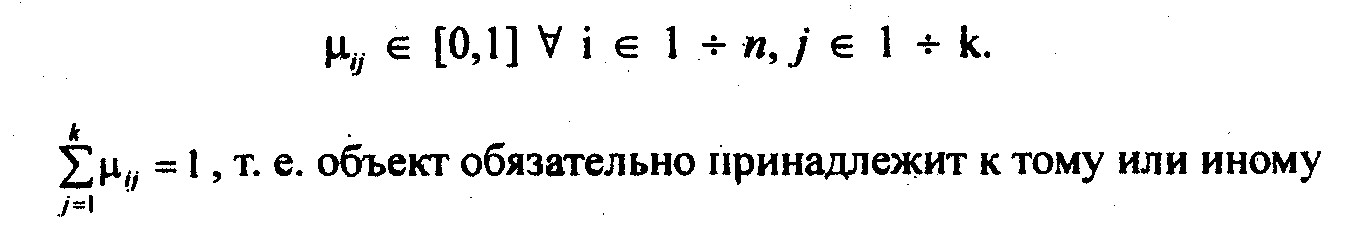
нечеткому множеству. Качество разбиения определяется как минимизацией внутриклассовой дисперсии, так и максимизацией удаленности центров классов.
Алгоритмы и программы многомерной классификации постоянно развиваются: разрабатываются ППП, учитывающие размытость границ между классами (распознавание в нечетких множествах), различную длину описаний классов и т. д. Большое значение в решении задач иерархических классификаций имеет компьютерная графика - так называемые классификационные деревья. Подробнее вопросы многомерной классификации освещаются в работах, указанных в списке рекомендуемой литературы.
|